e(ネイピア数)=2.718……の意味
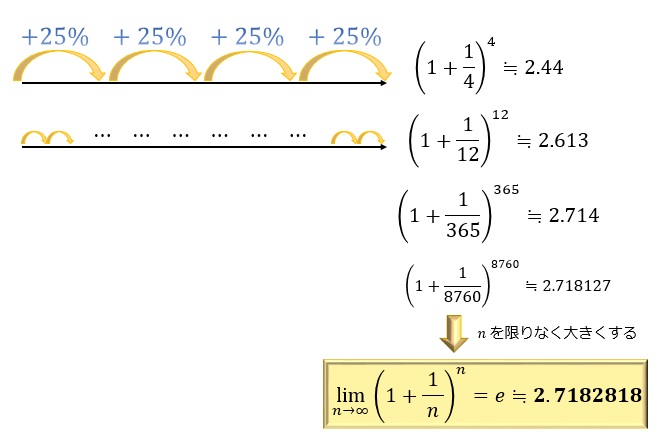
e(ネイピア数)の定義
e≒2.718というのは何となく習った気がする。
よく分ってなかったけど改めて意味を把握。
- 1年に1回、100%の金利がつく銀行があったとする。
元金を1とすると、1(100%)の利息が1回つく。
(1 + 1)の1乗=2
- 1年に2回、50%の金利がつく銀行があったとする。
元金を1とすると、1/2(0.5、50%)の利息が2回つく。
(1 + 1/2)の2乗=2.25
- 1年に3回、33.33%の金利がつく銀行があったとする。
元金を1とすると、1/3(0.3333、33.33%)の利息が3回つく。
(1 + 1/3)の3乗=2.370…… - …
… - 1年に∞回、1/∞の金利がつく銀行があったとする。
元金を1とすると、1/∞の利息が∞回つく。
(1 + 1/∞)の∞乗=2.718
1回あたりの金利が1/n、金利の支払いがn回、nが大きいほど、利息がついた後のお金が増える。
nが∞になったときの数字が2.718……
よく使う数字なので、2.718……と書くのめんどいし「e」って文字で代用しようぜってなったのがネイピア数e。
円周率の3.14をπと書くのと同じ感じ。
自然対数の底(ネイピア数) e の定義と覚え方。金利とクジの当選確率から分かるその使い道
![]()

自然対数の底(ネイピア数) e の定義と覚え方。金利とクジの当選確率から分かるその使い道|アタリマエ!
自然対数の底とは、\(2.71828\cdots\) と無限に続く超越数のこと。 小数表記で

コメント